 |
|||||||
|
|||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
 |
|
Matt Drummond website Edited by Robert Jan Kila. Html version remixed by RJK & DDR. German translation by Daniel Hartlehnert. |
|
Size:
0 ko
Platform: Mac/PC |
|
|
| Parametrische oszillation |
 Parametrisches ChaosHallo alle zusammen. Hier bin ich wieder mit einem netten kleinen Tutorial über das Animieren für die Faulen unter uns (hauptsächlich also für mich, daher die lange Zeit zwischen den Tutorials). Dieses Tutorial beschäftigt sich hauptsächlich mit den parametrischen Animationsfähigkeiten von EIU. Parametrisch? Seit wann haben wir denn dieses Feature, hör ich Euch schon sagen. Ungefähr seit Version 2.9 als wir den Function Curve Editor bekamen. Hier also nun, wie´s geht. Überblick Jedes Lebewesen bewegt sich in einem sich wiederholenden oder oszilierenden sinusartigen Muster. Ihr glaubt mir nicht? Nun, betrachtet mal den menschlichen Gang. Wir bewegen unsere Beine vor und zurück. Wir schwingen mit den Armen. Wir hüpfen hoch und runter während wir laufen (einige mehr als andere). Betrachtet andere menschliche Aktivitäten......phwaaarrrr.....oops.....tschuldigung. Wir lassen das Ganze lieber jugendfrei. Wie sieht das z.B. aus wenn Vögel fliegen? Die Flügel schwingen hoch und runter, der Körper bewegt sich in einer sinusförmigen Bewegung vom Kopf bis zum Schwanz. Wie siehts aus mit Fischen, Schlangen, Insekten, muss ich noch weiter gehen? Nein?.....Ok dann. Also, Lebewesen ganz allgemein, benutzen die bescheidene Sinuswelle um vorwärts zu kommen. Aber das Leben ist unvorhersagbar, chaotisch, zufällig.......komplex.....stimmts? Also wie kommt es, dass eine einfache Sinuswelle auch nur annähernd etwas natürliches und organisches simulieren kann? Mann, Ihr habt aber viele Fragen... Ein Beispiel Nehmen wir einen Stein, der in einen See geworfen wird. Wellen breiten sich konzentrisch aus, die aus einer perfekten Sinuswelle bestehen. Werft nun in Eurem geistigen Auge noch einen Stein in den See, und noch einen, und noch einen. Bald wird die perfekte Sinuswelle überlagert von ein paar anderen perfekten Sinuswellen mit unterschiedlichen Wellenlängen so dass das Ganze in einen mehr oder weniger zufällig aussehenden Haufen aus lauter kleinen Bergen verwandelt wird. In EIU kann man dies mit parametrischen Deformationen simulieren. Parametrisch? Einige von Euch fragen sich wahrscheinlich immer noch, was zum Teufel parametrisch bedeutet? Einfach ausgedrückt... man kann einzelne Parameter der Animation jederzeit ändern ohne dabei das Ganze zu zerstören, sich die Haare auszureissen, die Familie anzuschreien, die Katze zu treten und schließlich nochmal ganz von vorne anzufangen... Schaut mich nicht so an, das haben wir alle schonmal erlebt mit einer bestimmten Software die hier ungenannt bleiben wird. (räusperuniversehüstel... ;-) Parametrische Deformationen? Deformationen sind von Natur aus parametrisch denn jede Änderung die man an einen Deformationsparameter vornimmt wirkt sich auf alle anderen Deformationen aus und wird in Echtzeit angezeigt. Das erlaubt es uns, sich das Ganze in der letzen Minute nochmal anders zu überlegen ohne sich die Haare auszureißen, die Familie anzuschreien.....etc. |
 Ihr braucht dazu....Electric Image Universe. Einen Goldfisch, Schlange oder Eine Frau tuts auch. Diese zusätzlichen Objekte sind nur als Anhaltspunkt da. Ihr könnt damit rumspielen, aber vorsicht mit der Frau, denn die können beißen. |
Schritt 1: Fügt ein Ubershape hinzu. Macht daraus einen Quader X = 5, Y= 5, Z= 1000. Setzt die EI Divisions auf 50. |
Schritt 2: Fügt eine neue Deformationsregion hinzu und nennt sie "Sinus Welle". |
| Schritt 3: Fügt eine neue Deformation zu dieser Regionn hinzu und setzt Type auf Linear Wave. Setzt die Direction auf Z und Deform auf Y. Setzt die Amplitude auf 10. |
Schritt 4: Bei den Options für die Deformation setzt Waves auf 20. Lasst die Phase zunächst auf 0. |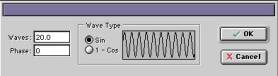
Schritt 5: Fügt eine weitere Deformation hinzu und wiederholt die Schritte 2 und 3. |
| Schritt 6: Bei den Options für die neue Deformation setzt die Waves auf 14. Belasst die Phase zunächst auf 0. Ihr werdet bemerken, dass die erste lineare Welle jetzt unterbrochen ist.  |
| Schritt 7: Fügt noch eine Welle hinzu. Diesmal, setzt die Wellenanzahl auf 9. Ihr werdet bemerkt haben, dass die Anzahl der Wellen sich nicht durcheinander teilen lassen. Dadurch wird mehr Zufälligkeit erzeugt..  |
|
|
| Schritt 8: Stellt die Zeit auf 4 Sekunden (wieso 4 Sekunden? Keine Ahnung, hört sich gut an. Verdammt, stellt sie auf 5 Sekunden wenn ihr wollt). |
Schritt 9: Stellt sicher, dass das kleine grüne Dreieck für das Ubershape an ist und öffnet die Deformationspalette. Bei jedem der linearen Deformationen stellt die Phase auf -360. Dies wiederholt die Welle einmal durch das ganze Objekt von vorne nach hinten. |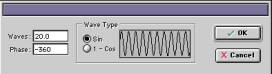
Schritt 10: Lasst Euch die Deformationsparameter für die Ubershapes im Projekt Fenster anzeigen. |
| Schritt 11: Öffnet jede Zeile mit den aufgelisteten Linear Waves und macht bei jeder einen Doppelklick um sie dem F-Curve Fenster hinzuzufügen. (Bem.: Mehr Info darüber findet Ihr in Eurer EIU PDF Dokumentation). |
| Schritt 12: Öffnet das F-Curve Fenster. Die Kurven Eurer Phasen sollten hier aufgelistet sein. |
Schritt 13: Macht einen Doppelklick auf jede der Phasen und stellt die rechte Wiederholung auf Accumulate. Die Wellen bewegen sich jetzt unendlich lange durch das Objekt.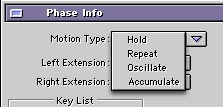 Wieso haben wir Accumulate benutzt? Wieso nicht einfach Repeat? ...wartet´s ab, ich komm gleich dazu. Im Moment bewegt sich die gesamte Form, die aus den sich überlagernden Sinuswellen ergibt durch das Objekt in einem Haufen. Das gefällt uns nicht. Das ist nicht organisch. Es ist nicht zufällig. |
Schritt 14: Selektiert die erste Phasenkurve und zieht das Ende nach unten, so dass v (Value) = 500. Wieso 500? Das ist wieder mal egal, geht nur sicher dass die Phase nicht teilbar durch einer der anderen Kurven ist.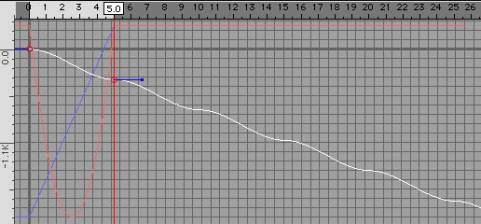 Jetzt bewegt sich diese Welle schneller durch das Objekt als die anderen. Wenn wir einfach nur Repeat benutzt hätten, hätten wir jetzt eine Welle die keinen vollen Zyklus vollendet sondern einfach wieder an den Anfang springt. |
| Schritt 15: Schaltet im Projekt Fenster die grünen Dreiecke für Wave und Frequency bei jeder Deformation aus. Dadurch können wir mit diesen Werten spielen ohne Keyframes zu setzten!! |
| Schritt 16: Bewegt die Zeit irgendwo hin und verändert die Phasenkurven um die Rate zu verändern. Schaut wie sich alles erneuert und fließt. Dass ist parametrisch. |
| Schritt 17: Benennt das Objekt "Pfad". |
| Schritt 18: Fügt ein neues Ubershape hinzu. Macht daraus eine Kugel mit Radius 5. Setzt die EI Divisions auf 20. Skaliert dieses Objekt auf 5 in Z Richtung. |
| Schritt 19: Öffnet das Link Info Fenster und aktiviert Inherit Deformation. |
| Schritt 20: Linkt das neue Ubershape an das Pfadobjekt. Schaltet das Pfadobjekt aus und klickt auf Preview. Voila! Jetzt könnt Ihr Eurer Pfadobjekt nach Belieben verändern und das Tochterobjekt wird automatisch upgedated. Ihr könnt auch die Position des Kindes animieren und die Deformationen werden sich darauf auswirken.  |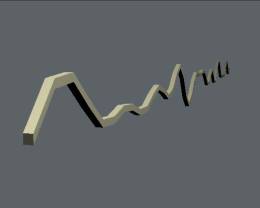
 Bem.: Alle Deformationen haben eine Bounding Region. Auch wenn diese nicht so eingestellt ist, den Effekt zu limitieren, werdet Ihr bemerken, dass wenn ein Tochterobjekt sich aus der Deformationsregion des übergeordneten Objektes heraus bewegt, der Effekt abgeschnitten wird. Das ist vor allem bei linearen Wellen bemerkbar. |
Nun, so viel bis hierher, Ihr schleimiger glitschiger Haufen. Denkt dran, Euch ab und zu mal auf dem EI Platter einzuloggen und in unseren Singsang einzustimmen. Bohemian Rhapsody war bisher unser Lieblingssong, aber wir halten immer Ausschau nach neuem Material.
Grüße,
Matt Drummond
 |